1. WGan-GP란
gan은 ai의 발전과정 중 가장 혁신적이라고 할 수 있다.
간단히 gan을 소개하자면 두 개의 모델의 경쟁 과정이라고 할 수 있다.
사람도 좋은 라이벌이 있다면 잘 성장하듯이
하나는 가짜 이미지를 만들어내는 generator 모델 , 다른 하나는 가짜 이미지를 구별해내는 discriminator모델을 생성하여 서로를 경쟁 시키면서 가짜 이미지를 만들어내는 모델을 더욱 정교화하는 모델이다.
요즘들어 GPT-3, GPT-4등 open AI의 거대 ai들이 핫하다. 이 거대 ai들은 데이터셋으로 부터 배우는 supervised learning도 수행하지만 텍스트로 부터 이미지를 만들어내고 그림의 화풍을 변화시키는 등 창작의 영역이 가능한 ai들이다. 이 모든 기술은 gan울 기반으로 하고 있다고 볼 수 있다.
WGAN-GP는 일반적인 gan의 loss function을 변형하여 구축했던 wgan에서 한 단계 더 발전한 모델이다. 이 처럼 gan 모델은 가짜 이미지와 진짜 이미지를 구별해내는 loss function하나의 차이로도 엄청난 성능 차이를 낼 수 있다. (학습이 불안정하다. )
1-1 WGAN
1-1-1 KL Divergence
Wgan-GP는 앞서 Wgan에서 발전한 모델이라고 하였다. Wgan은 기존 original gan이 사용하던 BCE Loss의 KL, JS발산 문제를 해결하기 위해 Wasserstein Distance라는 loss function을 도입한 모델이다.
gan은 원본 데이터들의 확률 분포와 생성된 가짜 이미지들의 확률 분포를 최소화 시키는 방향으로 학습이 진행된다. 이 때 이 확률 분포의 차이를 측정할 때 가장 많이 쓰이는 수식이 바로 KL-Divergence이다.
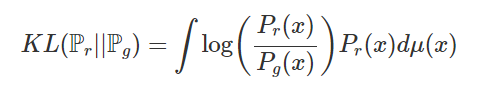
여기서 Pr은 원본 이미지의 확률 분포, Pg는 generating된 가짜 이미지의 확률 분포이다. 하지만 log함수안의 들어있는 분수식
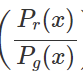
에서 Pg(x)가 만약 0에 수렴한다면 어떻게 될까 분수는 무한대가 될 것이고 단조 증가 함수인 log함수도 무한대로 발산하게 될 것이다. 또한 Pg(x)가 0이면서 Pr(x)가 0이 아니라면 식은 발산하게 된다. 많은 논문들에서 저차원의 아직 학습이 잘 되지 않은 gan의 경우 위와 같은 발산 문제가 빈번하게 발생한다고 한다.
만약 KL-Divergence 식이 발산한다면 두 확률 분포의 거리 또한 무한대로 발산하므로 원본에 가까운 확률 분포를 찾을 수가 없다. (우리는 두 확률 분포를 거의 일치시키는 것이 목표이기 때문이다. )
그래서 WGan에서는 위와 같이 두 확률 분포의 거리를 측정하는 방식을 변화시킨다.
1-1-3 JS Divergence
Js Divergence식은 위의 KL Divergence 식을 통해 나타낼 수 있다.
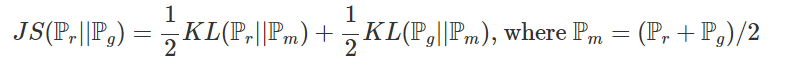
수식은 매우 복잡하니까 이해하기 보다는 경향성을 살펴보면 만약 Pm이 0이라면 Pr과 Pg또한 0이 되므로 무한대로 발산할 일은 생기지 않는다. (왜냐하면 Pr과 Pg는 모두 양수일 수 밖에 없기 때문이다. )
하지만 아예 두 분포가 전혀 겹치지 않는다면
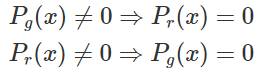
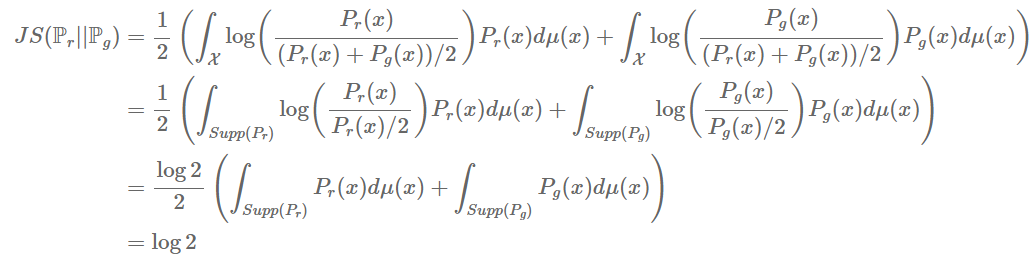
다음과 같은 수식 과정을 통해 log2로 수렴한다고 한다. 만약 log2로 수렴한다면 두 분포가 아주 멀리 존재해도 계속 log2이므로 얼마나 먼지에 대한 정보를 알 수가 없다.
수식 관련한 내용은 다음 블로그에 잘 정리가 되어있다.
https://haawron.tistory.com/21
1-2 WGAN의 문제
상식적으로 생각해봐도 드라마틱하게 변화하는 과정에서는 변수가 많이 일어날 수 밖에 없다.
그래서 WGAN의 두 확률 분포를 측정하는 수식은 다음과 같이 생겼다.
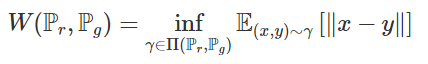
위의 loss를 Wasserstein loss라고 부른다. WGAN은 위의 wasserstein loss를 사용하여 WGAN이라고 불린다.
자세한 수학적 내용은 위의 블로그에 자세히 나와 있으니 참고하면 좋다.
그래서 WGAN-GP가 나왔으면 WGAN에 문제가 있기 때문에 나온 것이 아닐까?

논문에서 그 문제점을 찾을 수 있다. clip이라는 것은 update되는 W의 범위를 제한 시켜버린다는 것이다. 사람의 임의적인 판단이 들어가는 부분이다.
논문 내에서도 이 방법은 매우 좋지 않은 방법이라고 소개하고 있지만 성능이 잘 나왔기 때문에 논문이 나오게 되었다.
2. Wgan-GP
자 위에서 안전하게 두 확률 분포의 거리를 측정할 수 있는 wasserstein distance를 만들었지만 문제점이 있었다. 과정에서 업데이트 되는 W의 범위를 사람이 임의적으로 cliping해버리는 부분이었다.
방법은 cliping하는 대신 두 확률 분포 사이의 내분 점 중 하나를 sampling한 점을 사용하는 방법이다.
자세한 수학적 내용은 위의 블로그에 존재한다.

논문을 확인해봐도 아까 무식하게 cliping해버리던 부분이 사라지고 Loss Function또한 RMS에서 Adam으로 변경된 것을 확인할 수 있다.
따라서 아주 극한 상황에서도 WGAN-GP는 안정적으로 학습을 진행할 수 있다. (대신 천천히 배운다 -> 많은 epoch를 수행해야한다. )
내가 이 WGAN-GP를 선택한 이유는 현재 졸업 프로젝트로 진행 중인 아토피 피부 병변 중증도 개선 모델 때문이었다.
의료 데이터이다 보니 수집할 수 있는 데이터의 양이 많지 않았고 충분한 데이터가 존재하지 않으니 학습이 충분히 진행되지 않았다. 따라서 GAN으로 가짜 이미지를 생성한 후 GAN으로 생성한 이미지를 다시 개선한 Xception모델에 넣어서 학습을 진행하려고 했다.
그러려면 작은 데이터로도 안정적으로 학습을 진행할 수 있는 WGAN-GP모델이 좋을 것이라고 생각해 진행하게 되었다.
구현한 코드는 다음과 같다.
class ConvLayer(Layer):
def __init__(self, nf, ks, strides=2, padding='same', constraint=None, **kwargs):
super().__init__(**kwargs)
self.conv = Conv2D(nf, ks, strides=strides, padding=padding,
kernel_initializer='he_normal', kernel_constraint=constraint, use_bias=False)
# self.bn = BatchNormalization()
self.norm = LayerNormalization()
self.act = LeakyReLU(0.2)
def call(self, X):
X = self.act(self.conv(X))
return self.norm(X)
def conv_layer(nf, ks, strides=2, padding='same'):
conv = Conv2D(nf, ks, strides=strides, padding=padding, use_bias=False)
bn = BatchNormalization()
act = LeakyReLU(0.2)
return keras.Sequential([conv, act, bn])
def critic(input_shape=(128, 128, 3), dim=128, n_downsamplings=5):
h = inputs = keras.Input(shape=input_shape)
# 1: downsamplings, ... -> 16x16 -> 8x8 -> 4x4
h = ConvLayer(dim, 4, strides=2, padding='same')(h)
for i in range(n_downsamplings - 1):
d = min(dim * 2 ** (i + 1), dim * 8)
h = ConvLayer(d, 4, strides=2, padding='same')(h)
h = keras.layers.Conv2D(1, 4, strides=1, padding='valid', kernel_initializer='he_normal')(h)
h = Flatten()(h)
return keras.Model(inputs=inputs, outputs=h)downSampling을 진행하는 Discriminator 모델이다.
class UpsampleBlock(Layer):
def __init__(self, nf, ks, strides=2, padding='same', constraint=None, **kwargs):
super().__init__(**kwargs)
self.conv_transpose = Conv2DTranspose(nf, ks, strides=strides, padding=padding,
kernel_initializer='he_normal', kernel_constraint=constraint)
# self.bn = BatchNormalization()
self.norm = LayerNormalization()
self.act = ReLU()
def call(self, X):
X = self.act(self.conv_transpose(X))
return self.norm(X)
def deconv_layer( nf, ks, strides=2, padding='same'):
conv_transpose = Conv2DTranspose(nf, ks, strides=strides, padding=padding)
bn = BatchNormalization()
act = ReLU()
return keras.Sequential([conv_transpose, act, bn])def generator(input_shape=(1, 1, 128), output_channels=3, dim=128, n_upsamplings=5):
h = inputs = keras.Input(shape=input_shape)
d = min(dim * 2 ** (n_upsamplings - 1), dim * 8)
h = UpsampleBlock(d, 4, strides=1, padding='valid')(h)
# upsamplings, 4x4 -> 8x8 -> 16x16 -> ...
for i in range(n_upsamplings - 1):
d = min(dim * 2 ** (n_upsamplings - 2 - i), dim * 8)
h = UpsampleBlock(d, 4, strides=2, padding='same')(h)
h = keras.layers.Conv2DTranspose(output_channels, 4, strides=2, padding='same',
kernel_initializer='he_normal')(h)
h = keras.layers.Activation('tanh')(h)
return keras.Model(inputs=inputs, outputs=h)가짜 이미지를 생성해내는 generator모델이다.
2-1 두 모델 비교
나는 인풋 이미지를 128x128로 산정하고 모델을 구성했다. summary를 해보면 다음과 같다.
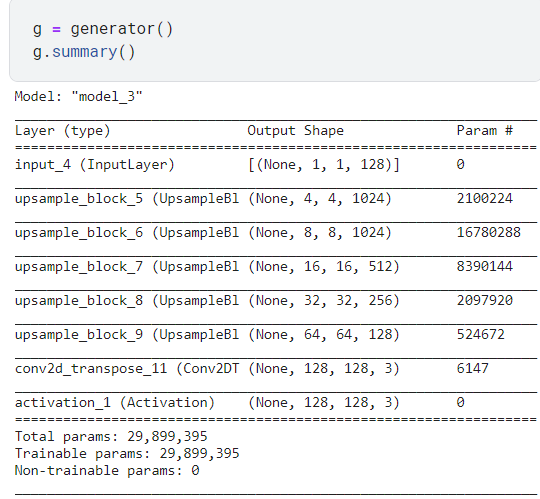
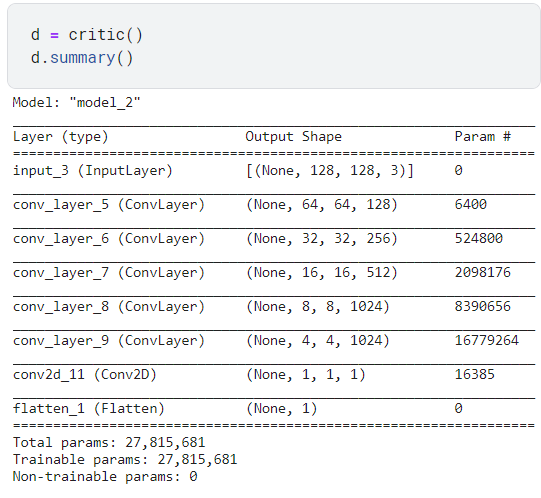
가장 큰 특징으로는 두 모델의 convolution layer들이 완벽히 대칭을 이룬다는 점이다.
하지만 128x128은 gan으로 생성하기에 큰 이미지인 거 같아 64x64로도 변경하여 실험을 진행할 예정이다.
2-2 loss
#Wasserstein loss
def d_loss(real, fake):
real_loss = -tf.reduce_mean(real)
fake_loss = tf.reduce_mean(fake)
return real_loss + fake_loss
def g_loss(fake):
return - tf.reduce_mean(fake)wasserstein loss function 이다.
@tf.function
def gradient_penalty(model, real, fake):
shape = [tf.shape(real)[0]] + [1, 1, 1]
alpha = tf.random.uniform(shape=shape, minval=0, maxval=1)
interpolated = alpha * real + (1-alpha) * fake
with tf.GradientTape() as tape:
tape.watch(interpolated)
pred = model(interpolated)
grad = tape.gradient(pred, interpolated)
norm = tf.norm(tf.reshape(grad, [tf.shape(grad)[0], -1]), axis=1)
gp = tf.reduce_mean((norm - 1.)**2)
return gpgradient의 penalty를 부여해주는 함수이다.
optD = tf.keras.optimizers.Adam(lr=0.0001, beta_1=0, beta_2=0.9)
optG = tf.keras.optimizers.Adam(lr=0.0001, beta_1=0, beta_2=0.9)두 모델의 loss function으로는 논문에서도 사용한 Adam을 사용해주었다.
@tf.function
def trainD(real):
noise = tf.random.normal((BATCH_SIZE, 1, 1, noise_dim))
with tf.GradientTape() as tape:
fake_images = g(noise, training=True)
real_output = d(real, training=True)
fake_output = d(fake_images, training=True)
gp_loss = gradient_penalty(functools.partial(d, training=True), real, fake_images)
loss = d_loss(real_output, fake_output)
disc_loss = loss + 10 * gp_loss
d_grad = tape.gradient(disc_loss, d.trainable_variables)
optD.apply_gradients(zip(d_grad, d.trainable_variables))
@tf.function
def trainG():
noise = tf.random.normal((BATCH_SIZE, 1, 1, noise_dim))
with tf.GradientTape() as tape:
generated_images = g(noise, training=True)
loss = g_loss(d(generated_images))
g_grad = tape.gradient(loss, g.trainable_variables)
optG.apply_gradients(zip(g_grad, g.trainable_variables))트레인 함수를 정의해주고
seed = tf.random.normal((16, 1, 1, 128))
def generate_images(model, epoch, test_input):
predictions = model(test_input, training=False)
fig, ax = plt.subplots(4, 4, figsize=(10,10))
for i, a in enumerate(ax.flat):
a.imshow(predictions[i, :, :, :])
a.axis('off')
plt.show()랜덤한 시드를 넣어준 후 이미지를 생성해서 보여준다.
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for image_batch in tqdm.tqdm(dataset, total=TOTAL//BATCH_SIZE):
trainD(image_batch)
if optD.iterations.numpy() % 5 == 0:
trainG()
display.clear_output(wait=True)
generate_images(g, epoch + 1, seed)
print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))그 후 파이썬의 tqdm라이브러리를 통해 for문이 진행되는 과정을 시각적으로 표현하였다.

100 epoch가 진행되었을 과정이다. 살짝의 사람의 피부색을 띄는 것을 확인할 수 있었다.
아마 WGAN은 학습과정이 매우 느리기 때문에 10000은 넘겨야 하지 않을까 싶다. 업데이트 되는 대로 수정하겠다.

800 epoch 상태이다. 이전보다 피부의 형태가 조금씩 생겨나는 것을 확인할 수 있다.

1100epoch 상태이다. Wgan은 특성상 진동이 많이 생기는 경향이 있는데 epoch가 진행되면서 질감이 좀 뭉개지기 시작하는 거 같다.
500epoch를 더 돌렸을 때의 모습이다.

몇 몇 이미지들은 정말 피부에 생긴 상처와 비슷해지고 있다.
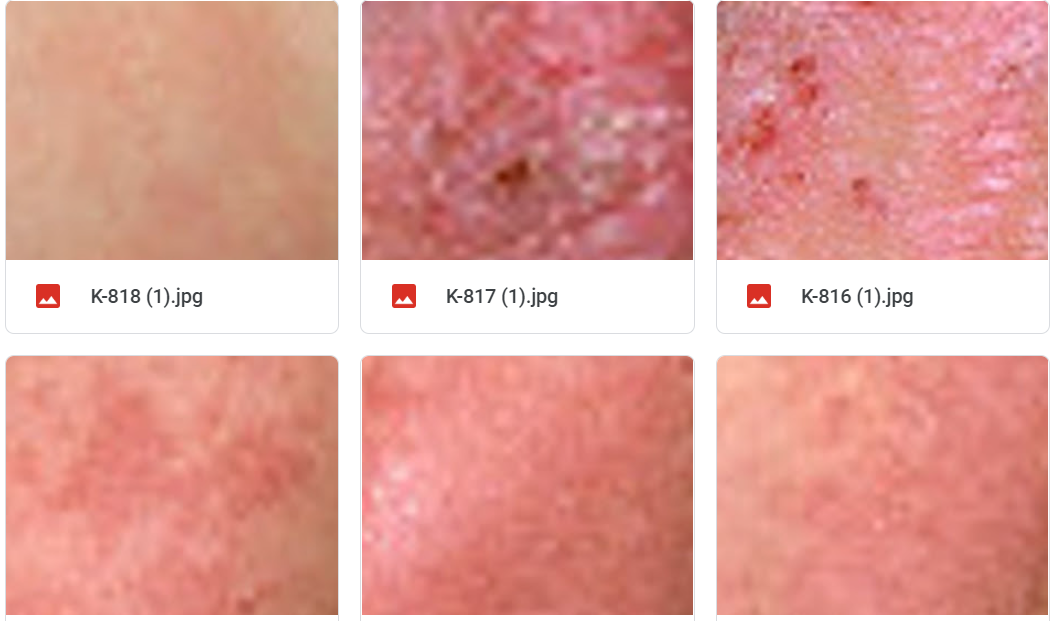
이것이 내가 학습시킨 이미지인데 점점 비슷해져가고 있다.
'파이썬 > ai' 카테고리의 다른 글
| [Ai, Python] Streamlit을 이용한 모델 시각화-7 (인천광역시 집 값 예측) (2) | 2022.06.26 |
|---|---|
| [Ai, Python] XGBOOST 회귀 모델 만들기 6 (2) | 2022.06.26 |
| [Ai, Python] 인천광역시 집 값 예측 프로젝트 - Feature Engineering (0) | 2022.06.25 |
| [ai, python] IMDB데이터베이스의 리뷰 데이터와 RNN을 이용한 리뷰 감성 분류하기 (3) | 2022.05.29 |
| [ai, python] - Image분류 by CNN (2) | 2022.05.29 |


댓글