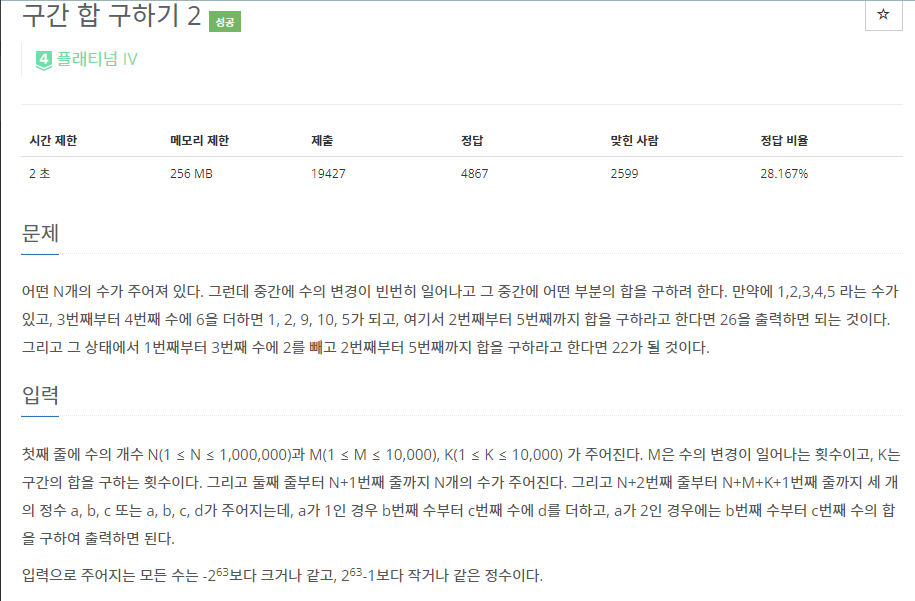
1. 문제
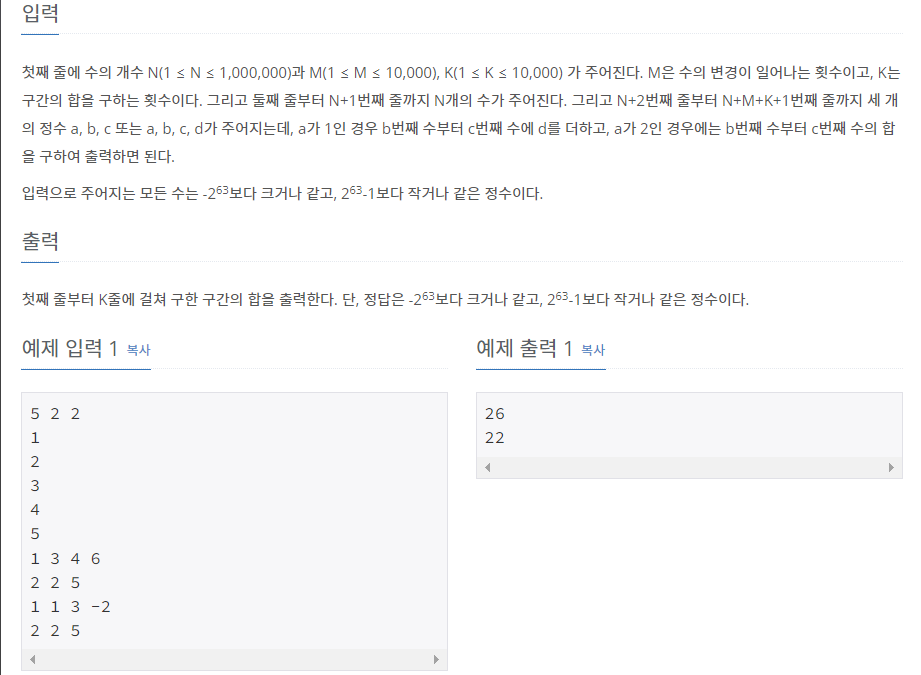
2. 입출력 및 예제
3. 문제 해설
이 문제는 백준 2042 구간합구하기 문제와 거의 동일하다. 단 하나 차이점이 있다면 이 문제에서는 단 하나의 수를 교체하는 것이 아니라 2번째 수부터 8번째 수를 9로 변경해 등과 같이 구간이 업데이트 된다는 점이다. 이 경우 최악의 시간복잡도는 처음부터 끝 구간을 변경하는 경우가 되고 update하는 데 드는 시간이 O(NlogN)이 된다.
이 문제에서 N은 백만이고 O(NlogN) 은 백만 * 1000 = 10억 번의 연산을 해야한다는 것이다. 대략적으로 c++언어로 1초라는 제한시간안에 통과하려면 1억번 정도의 연산을 수행해야하는데 위의 연산 횟수는 터무니 없다고 할 수 있다.
따라서 이 문제는 일반적인 세그먼트 트리의 update를 적용해서는 안된다.
lazy_loading이라는 새로운 개념을 도입해야한다.
https://yabmoons.tistory.com/442
[ Lazy Propagation ] 개념과 구현방법 (C++)
이 글에서는 'Lazy Propagation' 방법에 대해서 이야기를 해보자. 1. Lazy Propagation ??먼저 이 글을 읽기 전에 '세그먼트트리(SegmentTree)' 에 대해서 모른다면 세그먼트트리에 대해서부터 알아보고 오자.세
yabmoons.tistory.com
해당 블로그에서 많은 도움을 얻었다.
lazy_update란 말그대로 느리게 업데이트되는 세그먼트트리이다.
세그먼트 트리가 값을 도출해내는 과정을 생각해보자
세그먼트 트리는 항상 세 가지 경우를 생각해가면서 update를 하거나 query값을 구한다.
- 현재 노드가 대표하는 구간이 우리가 구하려고 하는 구간과 완전히 겹치지 않는 경우
- 현재 노드가 대표하는 구간이 우리가 구하려고 하는 구간에 완전히 포함되는 경우
- 현재 노드가 대표하는 구간이 우리가 구하려고 하는 구간에 일부만 걸쳐있는 경우
세그먼트 트리 함수의 query과정을 보면 다음과 같은 세가지 경우를 모두 고려해 답을 구하는 것을 알 수 있다.
long long query(int node, int start, int end, int left, int right) {
//node는 node번호 start, end 는 현재 노드가 대표하고 있는 구간 left, right는 우리가 구하고자 하는 구간
//1. 완전히 겹치지 않는 경우
if(left > end || right < start) return 0; // 완전히 겹치지 않으면 구하고자 하는 연산의 항등원을 리턴한다 여기서는 합을 구하므로 0을 리턴
//2. 완전히 포함
if(left <= start && right >= end) return Tree[node]; // 완전히 포함된다면 그 트리 노드를 리턴하고 자식 노드로 더 이상 이동하지 않는다.
//3. 일부만 겹칠 때는 더 탐색을 진행
int mid = (start + end) /2;
ll leftResult = query(node * 2, start, mid, left, right);
ll rightResult = query(node * 2 +1, mid+1, end, left, right);
return leftResult + rightResult;
}update의 경우도 마찬가지이다.
void update(int node, int start, int end, int idx, int diff) {
//1. 완전히 겹치지 않은 경우
if(end < idx || start > idx) return;
//2. 일부라도 포함되는 경우
Tree[node] += diff;
if(start != end) {
// 리프노드가 아니라면 더 탐색을 진행
int mid = (start + end) /2;
update(node * 2, start, mid, ldx, diff);
update(node * 2 + 1, mid+1, end, idx, diff);
}
}update의 경우 리프노드가 나올 때까지 탐색을 진행한다.
근데 매번 이렇게 리프노드까지 업데이트를 할 필요가 있을까?
구간으로 업데이트가 되는 경우에도 각 인덱스마다 다른 값이 더해지는 것이 아니라 같은 값이 더해진다. 예를 들면 3번 인덱스부터 9번 인덱스에 5를 더해줘와 마찬가지이다. 3번은 4로 6번 인덱스는 8로 바꿔줘와 같이 업데이트 되지 않는다.
따라서 우리가 구하고자하는 범위에 완전히 포함되는 최초의 노드가 나온다면 그 노드는 더 이상 자식으로 내려가며 업데이트해주지 않고 그 노드를 업데이트 해준 후 자신의 자식들의 업데이트 예정 값만 전달해주면 된다.
이 예정 값을 저장해주기 위해 나는 Tree만한 배열을 하나 더 선언해주었다.
생각해보면 세그먼트 트리도 트리이고 이 트리는 노드별로 자신이 대표하는 구간을 알 수 있다는 특징이 있다. 따라서 이 노드가 구간에 얼마나 포함이 되고 우리가 구하고자 하는 범위 중 얼마만큼을 포함하는 지를 알 수 있다는 뜻이다.
또한 노드를 방문했을 때 lazy값이 이미 존재한다면 lazy값을 먼저 업데이트 해준 후 추후 작업을 수행해야한다. lazy_update는 다음과 같이 진행할 수 있겠다.
void lazy_update(int node, int start, int end) {
// lazy값이 존재한다면
if(lazy[node]) {
Tree[node] += (end - start + 1) * lazy[node]; // 구간만큼의 노드를 대표하고 있으므로 그만큼 * 된 값이 업데이트 되어야한다.
if(start != end) {
// 만약 리프노드가 아니라면 lazy값을 자식들에게 전달해주어야한다.
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
// update를 해주었으므로 다시 0으로 만들어준다.
lazy[node] = 0;
}
}그렇다면 update과정은 어떻게 변화될까? 우리는 기존 특정한 index의 값을 변경하는 업데이트만을 진행했지만 이젠 구간을 업데이트 해야한다. 따라서 받는 인자도 우리가 구하고자 하는 구간이 추가될 것이다.
void update(int node, int start, int end, int left, int right, long long val) {
lazy_update(node, start, end); // lazy값이 있다면 먼저 lazy update진행
//1. 구하고자 하는 구간과 노드가 대표하는 구간이 완전히 겹치지 않는 경우
if(end < left || right < start) return;
//2. 구하고자 하는 구간안에 노드가 대표하는 구간이 완전히 포함되는 경우
if(start >= left && right >= end) {
Tree[node] += (end - start + 1) * val; // 우선 그 트리 노드를 업데이트 해준 후
if(start != end) { // 리프노드가 아니어야 자식이 존재
lazy[node * 2] += val;
lazy[node * 2 + 1] += val; // 자식 노드를 더 이상 탐색하지 않고 lazy값만 저장해준 후 리턴
}
return;
}
//3. 일부만 겹칠 땐 더 탐색을 진행해야함
int mid = (start + end) / 2;
update(node * 2 , start , mid, left, right, val);
update(node * 2 + 1, mid + 1, end, left, right, val);
Tree[node] = Tree[node * 2] + Tree[node * 2 + 1]; //만약 리프노드까지 가서 리턴되면 다시 업데이트 해주면서 올라온다.
}lazy_update함수를 통해 먼저 lazy값의 유무를 체크하고 구간 별 업데이트를 진행하는 것을 알 수 있다.
여기서 이전 update함수에 비해 시간을 줄일 수 있는 점은 만약 구하고자 하는 구간안에 완전히 포함되는 노드가 나온다면 lazy값 만을 자식들에게 전달해준 후 더 이상 탐색을 진행하지 않는다는 것이다.
query 함수를 통해 값을 구할 때도 lazy값을 먼저 확인해야한다. 만약 lazy값이 존재한다면 아직 업데이트가 되지 않은 노드라는 뜻이니까 값이 다르게 나올 수 있기 때문이다.
long long query(int node, int start, int end, int left, int right) {
//먼저 lazy 값 확인
lazy_update(node, start, end);
//1. 완전히 겹치지 않는 경우 구하고자 하는 연산의 항등원 리턴
if(left> end || right < start) return 0;
//2. 완전히 포함되는 경우
if(start >= left && end <= right) return Tree[node]; //자식노드로 이동하지 않고 그 노드를 리턴한다.
//3. 일부만 겹치는 경우 자식으로 탐색 진행
int mid = (end - start) / 2;
ll leftResult = query(node * 2, start, mid, left, right);
ll rightResult = query(node * 2 + 1 , mid+1, end, left, right);
return leftResult + rightResult;
}4. 코드
#pragma warning (disable : 4996)
#define ll long long
#define MAX 1000000
#define SIZE_TR 2097152
#include <cstdio>
int N, M, K;
ll origin[MAX + 2];
ll Tree[SIZE_TR];
ll lazy[SIZE_TR];
using namespace std;
ll initTree(int node, int start, int end) {
if (start == end) return Tree[node] = origin[start];
int mid = (start + end) / 2;
ll leftResult = initTree(node * 2, start, mid);
ll rightResult = initTree(node * 2 + 1, mid + 1, end);
return Tree[node] = leftResult + rightResult;
}
void lazy_update(int node, int start, int end) {
if (lazy[node]) {
Tree[node] += (end - start + 1) * lazy[node];
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
void update(int node, int start, int end, int left, int right, ll val) {
lazy_update(node, start, end);
if (right < start || left > end) return; // 아예 겹치지 않는 경우
if (start >= left && end <= right) {
//완전히 포함되는 경우라면
Tree[node] += (end - start + 1) * val; // 자기 자신을 업데이트한다.
if (start != end) {
lazy[node * 2] += val;
lazy[node * 2 + 1] += val;
}
return;
}
int mid = (start + end) / 2;
update(node * 2, start, mid, left, right, val);
update(node * 2+1, mid + 1, end, left, right, val);
Tree[node] = Tree[node * 2] + Tree[node * 2 + 1];
}
ll query(int node, int start, int end, int left, int right) {
lazy_update(node, start, end);
if (left > end || right < start)return 0;
if (left <= start && right >= end) return Tree[node];
int mid = (start + end) / 2;
ll leftResult = query(node * 2, start, mid, left, right);
ll rightResult = query(node * 2 + 1, mid + 1, end, left, right);
return leftResult + rightResult;
}
int main() {
scanf("%d %d %d", &N, &M, &K);
for (int i = 0; i < N; i++) {
scanf("%lld", &origin[i]);
}
initTree(1, 0, N - 1);
for (int i = 0; i < M + K; i++) {
int a, b, c; ll d;
scanf("%d", &a);
if (a == 1) {
scanf("%d %d %lld", &b, &c, &d);
update(1, 0, N - 1, b - 1, c - 1, d);
}
else {
scanf("%d %d", &b, &c);
printf("%lld\n", query(1, 0, N - 1, b - 1, c - 1));
}
}
return 0;
}
'c++ > 알고리즘' 카테고리의 다른 글
| [c++] 백준 - 2014 소수의 곱 (우선순위 큐) (0) | 2023.02.16 |
|---|---|
| [C++] 백준 - 11779 최소비용구하기2 (다익스트라) (0) | 2023.02.15 |
| [c++] 백준 - 11066 파일 합치기 (dp) (0) | 2023.02.14 |
| [c++] 백준 - 1520 내리막길 (DFS + DP) (0) | 2023.02.14 |
| [c++] 백준 - 단절점(11266) [단절점 이론] (0) | 2023.02.13 |


댓글