1. 문제
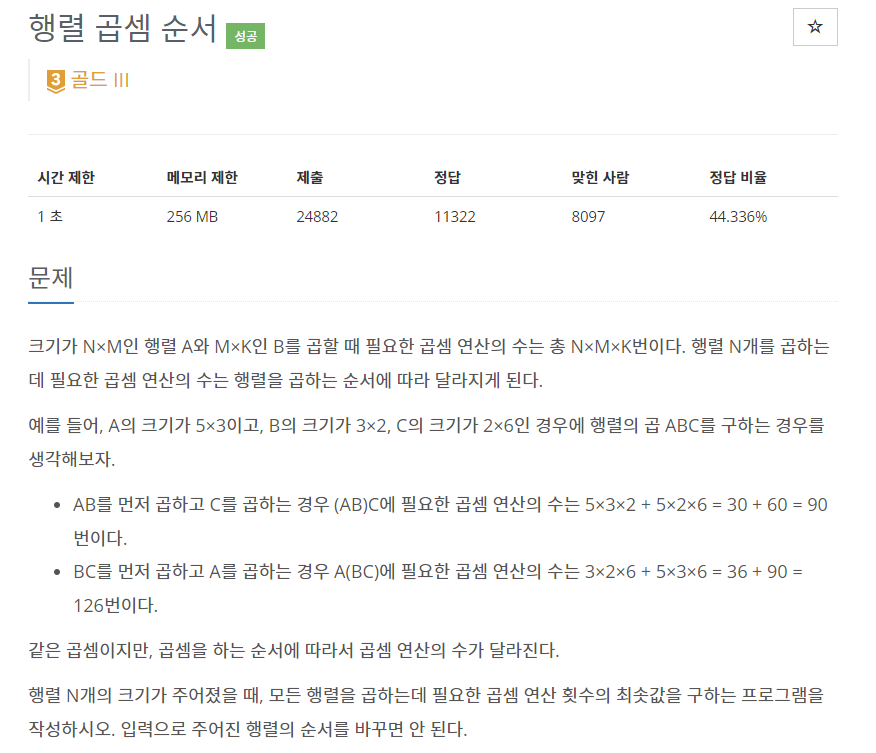
2. 입출력 및 예제
3. 문제 해설
dp문제이다. 그리고 여태까지 dp배열을 채우던 방식과는 조금 다른 형태이다.
대부분의 dp문제에서는 가로 방향으로 dp배열을 채우거나 세로 방향으로 dp배열을 채워갔다. 하지만 이 문제는 대각선으로 채워가야하는 문제이다.
dp문제를 풀 때는 세 가지 과정을 거쳐야한다고 했다.
- dp 배열의 정의
- 점화식 찾기
- 초기값 설정
나는 dp[i][i]를 i번째 배열에서 j번째 배열까지의 곱셈 연산 최소 횟수로 정의했다.
내가 생각한 점화식은 다음과 같다.
우선 행렬곱셈에 대해 알아보면
5 * 3 , 3 * 2, 2 * 6과 같이 세 행렬이 존재할 때 1번째로 가능한 곱셈의 경우는 앞의 두 행렬을 먼저 계산하고 마지막 행렬을 계산하는 것이다.
2번째로 가능한 곱셈의 경우는 마지막 두 개를 계산하고 앞의 행렬을 계산하는 것이다.
앞서 말한 두 가지 경우 중 1번째의 경우는 5 * 3 * 2 + 5 * 2 * 6 = 90번의 행렬 곱셈 량을 가지고
2번째의 경우는 3 * 2 * 6 + 5 * 3 * 6 = 126번의 곱셈량을 가져 같은 곱셈끼리도 다른 곱셈량을 가질 수 있다.
따라서 위의 식을 살펴보면 dp[1][3]은 첫 번째 행렬에서부터 3번째 행렬까지의 최소 행렬 곱셈량을 의미하는데
dp[1][3] = min(dp[1][3] , dp[1][2] + dp[3][3] + (Row[1] * Col[2] * Col[3]) , dp[1][1] + dp[2][3] + (Row[1] * Col[1] * Col[3])
에 해당한다. 따라서 중간의 경유점을 하나씩 이동해가며 위의 점화식을 갱신해가면 답이 나오게 되는 것이다.
또한 dp[1][3]은 dp[1][2]와 dp[2][3]의 값을 알아야 구할 수 있다. 즉, 채워가야하는 순서가 dp[1][2] -> dp[1][3]순이 아니라
dp[1][2] -> dp[2][3] -> dp[1][3]순이 되는 것이다.
더 많은 경우에서 dp[1][4]는 dp[1][2] -> dp[2][3] -> dp[3][4] -> dp[1][3] -> dp[2][4] -> dp[1][4] 순으로 구해져야한다.
따라서 dp배열이 대각선으로 채워지게 되는 것이다.
그럼 초기값은 어떻게 설정해야할까?
먼저 간격이 1만 차이나는 경우 그냥 행렬 곱셈의 양이 초기 값이 되겠다. dp[1][2]의 경우는 Row[1] * Col[1 or 2] * Col[2]가 초기 값이 되겠다. dp[1][1]과 같은 경우는 그냥 자기 자신이므로 0으로 초기값을 설정하면 될 것이다.
for(int i=1; i < N; i++) { //간격
for(int left = 1; left + i <= N; left++){
int right = left + i; // 끝 점
if(right > N) break;
dp[left][right] = INF; // 무한대로 초기화 (최솟 값을 구해줘야하므로)
for(int k = left; k < right; k++) { // 중간 경유지
dp[left][right] = min(dp[left][right] , dp[left][k] + dp[k+1][right] + (Row[left] * Col[k] * Col[right]))
}
}
}4. 코드
#pragma warning (disable : 4996)
#include <climits>
#include <cstdio>
#include <algorithm>
using namespace std;
int N, Row[501], Col[501]; // 행렬 저장
int D[501][501]; // dp
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; i++) {
scanf("%d %d", &Row[i], &Col[i]);
}
for (int i = 1; i < N; i++) { //간격
for (int left = 1; left < N; left++) { // 시작지점
int right = left + i;
if (right > N)break;
D[left][right] = INT_MAX;
for (int k = left; k < right; k++) { // 중간 경유지
D[left][right] = std::min(D[left][right],
D[left][k] + D[k + 1][right] + Row[left] * Col[k] * Col[right]);
}
}
}
printf("%d\n", D[1][N]);
}
'c++ > 알고리즘' 카테고리의 다른 글
| [c++] 백준-스도쿠 1520 - 백트래킹 (0) | 2023.02.13 |
|---|---|
| [c++] 백준 - 공장 (인덱스드 트리) (0) | 2023.02.09 |
| [c++] 백준-집배원 한상덕(이분탐색 , 투포인터) (0) | 2023.02.08 |
| [c++] 백준-LCA2 (Least Common Ancestor) (0) | 2023.02.08 |
| [c++] 백준-1865 웜홀 (벨만포드) (0) | 2023.02.07 |


댓글